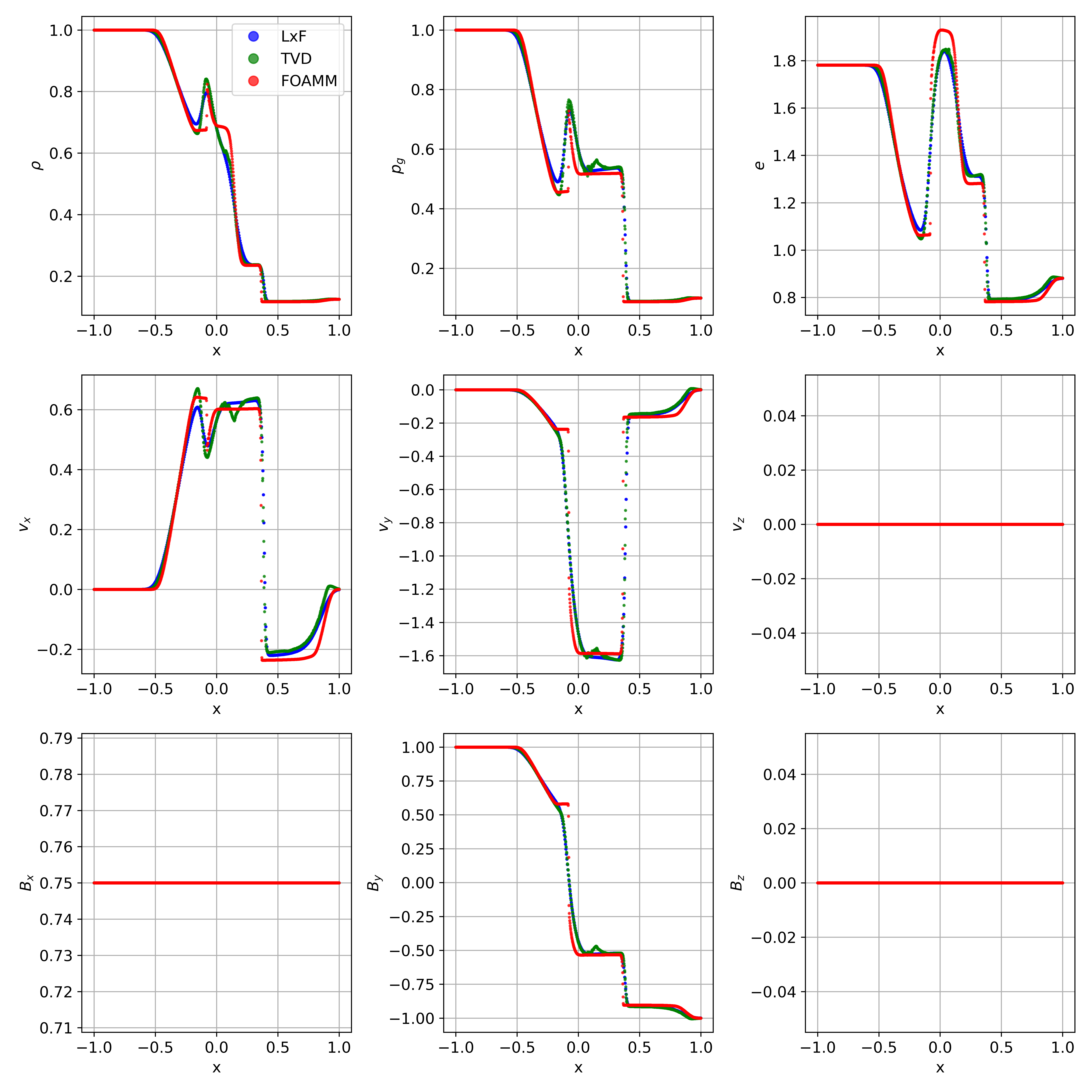
The code uses an upwind finite volume discretization for the ideal MHD equations in the conservative form. Several schemes approximate the numerical fluxes across the cell boundaries, namely:
- Lax-Friedrichs (LxF)
- Total Variation Diminishing Lax-Friedrichs (TVD)
- First Order Arithmetic Mean Matrix (FOAMM)
The figure below shows the simulation results at time t=0.2 s for the Brio & Wu problem [1] using 1000 cells. The general structure of the
solution is in agreement with those reported in the literature[1, 2], from left to right:
- Fast rarefaction (x = -0.27)
- Slow compound wave (x = -0.1)
- Contact discontinuity (x = 0.15)
- Slow shock (x = 0.36)
- Fast rarefaction (x = 0.9)
As expected, the schemes based on LxF show a more diffuse behaviour than the FOAMM scheme, which uses fewer cells to resolve the discontinuities.
References
- Brio, M. and Wu, C.C., 1988. An upwind differencing scheme for the equations of ideal magnetohydrodynamics. Journal of computational physics, 75(2), pp.400-422.
- Falle, S.A.E.G., Komissarov, S.S. and Joarder, P., 1998. A multidimensional upwind scheme for magnetohydrodynamics. Monthly Notices of the Royal Astronomical Society, 297(1), pp.265-277.
